Cryptography for Muggles 密碼學任督二脈

CX3302024-06-272024-10-18

前言

為甚麼會想寫這篇文

因為自己在學習的時候一直覺得密碼學是個很困難的領域，所以決定自己把一些筆記給記錄下來。一來是幫助自己以後可以回來翻，其次也希望可以幫助到正在學習密碼學的人！加油啦！

柯克霍夫原則 Kerckhoffs’s principle

“A cryptosystem should remain secure even if an adversary knows all the details of the system, except for the secret decryption key.” — Kerckhoffs’s principle

柯克霍夫原則是由 Auguste Kerckhoffs 在 19 世紀提出的，其內容主要就是說明一個好的加密系統即使其運作原理全部都是公開的，只要金鑰未公開，他就應該要是安全的。資訊理論的創始人 Claude Shannon 將其改說為以下說法。

“The enemy knows the system” — Claude Shannon

也就是說，永遠預設敵人知道你的整個加密系統是如何運作的，包括其中的算法以及各種原理。一個加密系統要在這樣的情境下還能保證其加密資料的安全性才稱得上是安全的。

領域展開：密碼學的三大領域

在密碼學中的任何知識幾乎都是圍繞著編碼、雜湊、加密這三個領域，所以就先來分別簡單聊聊他們各自都是甚麼吧！（這裡推薦一篇文章，講的滿深入淺出的：一次搞懂密碼學中的三兄弟 — Encode、Encrypt 跟 Hash）

編碼 Encoding

編碼的目的是為了資料的傳輸或表達，把原本的資料換一種方式表達而已。因為他只是把資料轉換成另一種形式，所以編碼後的資料仍然可以被解碼（Decode），也就是說整個過程完全是可逆的。

所以這裡要特別注意。編碼不是加密！編碼不是加密！編碼不是加密！

雜湊 Hashing

雜湊，又名哈希（對就是直接從 Hash 直接翻過來）。雜湊的話主要是用於數據校驗以及數據完整性的驗證，還有一些其他的安全應用比如數位簽章等。雜湊算法會有以下的特性：

不可逆性：雜湊的算法是不可逆的，無法透過已知的雜湊值（哈希值 Hash values）回推原始資料。
固定長度輸出：不管輸入的數據長度為何，哈希函式都會生成固定長度的哈希值。比如 SHA-256 的輸出長度就是固定 256 個 Bits。
唯一性：理想情況下，兩個不同的輸入會產生不同的輸出（避免碰撞）。

加密 Encryption

加密就相對好理解啦！就是用於保護數據的機密性（Confidentiality），確保只有被授權的用戶才能訪問數據。其加密和解密的過程都依賴於密鑰（Key），密鑰的保密性也會直接的影響到數據的安全性。

就好比是一個保險箱，要打開它需要一把鑰匙，而那把鑰匙就是密鑰。如果密鑰被盜取，那麼保險箱也就毫無用處了。

常見編碼 Common Encoding

ASCII Encoding

簡介

這應該大家都很熟悉吧！他的全名是 American Standard Code for Information Interchange，反正不是很重要，就是一個挺常見的編碼方式。以下是一張 ASCII 表：

Python Code

# 將字符串轉換為 ASCII 編碼
def ascii_encode(input_string):
    return [ord(char) for char in input_string]

# 將 ASCII 編碼轉換回字串
def ascii_decode(ascii_codes):
    return ''.join(chr(code) for code in ascii_codes)

# 示例
input_string = "This is ASCII encoding"
ascii_encoded = ascii_encode(input_string)
ascii_decoded = ascii_decode(ascii_encoded)

print("Original string:", input_string)
print("ASCII encoded:", ascii_encoded)
print("ASCII decoded:", ascii_decoded)

Base64 Encoding

簡介

Base64 通常用於傳輸二進制數據的場合，例如在電子郵件中嵌入圖像、文件等。它的範圍是從使用A-Z、a-z、0-9，共 62 個字符，加上兩個額外字符+和/，共 64 個字符。

原理

Base64 編碼這個名稱代表著它基於 64 個可列印字元所形成的編碼。由於 $\log_{2}64=6$ ，所以每 6 個位元（Bit）為一個基本單元，對應著一個可列印字元。每 3 個位元組（Byte）為 24 個位元，相當於 4 個 Base64 基本單元，代表每 3 個位元組可以由 4 個可列印字元表示。下圖就是每個可列印字元所對應的索引值。

Python Code

import base64


def base64_encode(data):
    # 使用 base64 模組的 b64encode 函式進行編碼
    encoded_bytes = base64.b64encode(data)
    # 將編碼後的位元組轉換為字串並回傳
    return encoded_bytes.decode("utf-8")


def base64_decode(encoded_data):
    # 將 Base64 編碼的字串轉為位元組
    encoded_bytes = encoded_data.encode("utf-8")
    # 用 base64 的 b64decode 解碼
    decoded_bytes = base64.b64decode(encoded_bytes)
    # 回傳解碼後的字串
    return decoded_bytes.decode("utf-8")

# 測試
data_to_encode = b"This is Base64 encoding"

encoded_data = base64_encode(data_to_encode)
print("Base64 Encoded Data:", encoded_data)

decoded_data = base64_decode(encoded_data)
print("Base64 Decoded Data:", decoded_data)

延伸

除了 Base64 編碼以外，這個 Base 家族還有許多例如 Base16（Hex）、Base32、Base58（用於 Bitcoin）等不同的編碼方式。如果有興趣的話歡迎閱讀這篇文章。

URL Encoding

簡介

URL Encoding 也稱作為 Percent-encoding，是一種將 URL 中的特殊字符和非 ASCII 字符轉換為百分號（%）後跟兩個十六進制數字的形式，以確保這些字符在 URL 中能夠被正確解析和傳輸。

Python Code

import urllib.parse

# URL 編碼
def url_encode(input_string):
    return urllib.parse.quote(input_string)

# URL 解碼
def url_decode(encoded_string):
    return urllib.parse.unquote(encoded_string)

# 示例
input_string = "This is URL encoding"
url_encoded = url_encode(input_string)
url_decoded = url_decode(url_encoded)

print("Original string:", input_string)
print("URL encoded:", url_encoded)
print("URL decoded:", url_decoded)

小結

這裡面其實在打 CTF 的時候最常用到的就是 Base64 了，所以其實只要熟悉一下 Base64 的原理還有代碼，在比賽的時候可以快速編碼解碼就可以啦！

常見雜湊函式 Common Hash Functions

如果想要了解一下哈希函式還有數位簽章的大致運作流程，可以在往下看之前先看一下這部影片。我自己認為它的內容簡單而且李永樂老師教的很清晰，幾乎沒有任何數學難度就可以理解！十分推薦去看！

MD5

簡介

MD5 的全名是 Message Digest Algorithm 5，它能將任意長度的數據轉換為 128 位（16 Bytes）長度的哈希值。它的運算過程如下：

填充資料
- 將資料的末尾添加一個"1"，為了標記填充的開始；然後添加足夠位的"0"，使資料的長度（以 Bit 為單位）對 512 取模後的結果為 448。這樣可以確保最終加上 64 位長度信息後，總長度是 512 的整數倍。
- 最後，將消息的原始長度（以位為單位）附加到消息的末尾，使得填充後的消息長度為 512 的倍數。
初始化 MD 緩衝區
- MD5 使用四個 32 位的變量（A, B, C, D）來存儲中間和最終的雜湊值。它們分別初始化為：
  - A = 0x67452301
  - B = 0xEFCDAB89
  - C = 0x98BADCFE
  - D = 0x10325476
處理資料
- 將填充後的資料以 512 位（64 Bytes）分成多個塊（Chunk）。
- 對於每個 512 位的塊，再分為 16 個 32 位的小塊。
- 用這些 32 位的小塊和上面初始化好的四個 32 位的變量（A, B, C, D），進行四輪（每輪 16 步）迭代運算。每一步使用非線性函數（F, G, H, I）和特定的常數以及循環左移操作，來混淆和壓縮數據。公式如下：
  $\begin{align*} &F(X, Y, Z) = (X \land Y) \lor (\neg X \land Z) \\ &G(X, Y, Z) = (X \land Z) \lor (Y \land \neg Z) \\ &H(X, Y, Z) = X \oplus Y \oplus Z \\ &I(X, Y, Z) = Y \oplus (X \lor \neg Z) \\ &\oplus, \land, \lor, \neg \text{ are the signs of XOR, AND, OR, NOT} \end{align*}$
輸出最終哈希值
- 最終將四個 32 位的變量 A, B, C, D 串聯起來成為一個 128 位的哈希值（以小端序表示）。

看完文字敘述之後我們來看一下 MD5 的圖解吧！

看完了那麼多可能有點頭昏腦脹，但沒關係！慢慢理解它的過程還有大致流程，多看幾次可能就比較理解了。接下來講點比較簡單理解的東西吧！甚麼是 Endian？

端序 Endian

在了解端序是甚麼之前，我們先來講個有趣的吧！

「endian」一詞來源於十八世紀愛爾蘭作家喬納森·斯威夫特（Jonathan Swift）的小說《格列佛遊記》（Gulliver’s Travels）。小說中，小人國為水煮蛋該從大的一端（Big-End）剝開還是小的一端（Little-End）剝開而爭論，爭論的雙方分別被稱為「大頭派（Big-Endians）」和「小頭派（Little-Endians）」。（From Wikipedia）

好了這真的十分不重要但還是滿有趣的 XD。進入正題吧！

端序，又稱位元組順序，又稱尾序。它指的是排列位元組的順序或方式。它又分為以下兩種：

大端序 Big-Endian
小端序 little-Endian

那他們具體又有甚麼差別呢？下面一張圖看完馬上可以理解其中的差別在哪！

如果這張圖還是不能理解，那我們再看下一張圖！

如果看圖片看不太懂，那就用文字來介紹一下。

首先，要先知道甚麼是 LSB 和 MSB，LSB 是最低有效位（Least Significant Bit，LSB）；MSB 是最高有效位（Most Significant Bit，MSB）。和十進制類似，通常 MSB 是二進制數的最左側，而 LSB 位於最右側。

而大端序就是是從數據的 MSB 作為起始位置；而小端序是從最低有效位 LSB 開始。

那大端序和小端序在應用上有甚麼差別呢？

大端序
- 更加直觀
- 應用於一些網絡協議中，例如 TCP/IP
小端序
- 更符合計算機科學中的數學計算順序，因為最低有效位在前面更方便處理。（像是數據型態的轉換）

端序的部份我就大致介紹到這邊。如果對端序有興趣想要更深入了解的話，可以去看這篇文章！

Python Code

import hashlib

# 要雜湊的消息
message = "This is MD5!"

# 創建一個 MD5 雜湊對象
md5_hash = hashlib.md5()

# 將消息編碼後更新到雜湊對象中
md5_hash.update(message.encode())

# 獲取雜湊值（十六進制表示）
hash_hex = md5_hash.hexdigest()

# 打印雜湊值
print(f"MD5 value: {hash_hex}")

MD5 已死

為甚麼說 MD5 已死呢？在 2004 年，中國的密碼學家王小雲和其研究同事發表了一篇論文，詳細描述了如何在不到一個小時內找到 MD5 的碰撞，同時這也證明了 MD5 是不安全的。

2012 年的時候密碼學研究人員 Marc Stevens 提出了一種更高效的 MD5 碰撞攻擊方法，稱為 Fast Collision Attack on MD5，他還開發了一個名為 HashClash 的工具，用於自動化生成 MD5 碰撞。

想更詳細的了解其原理，可以觀看以下影片！

SHA-256

簡介

SHA(Secure Hash Algorithm)家族的雜湊函式是被美國聯邦資訊處理標準（FIPS）所認證的安全雜湊算法。他們（SHA 家族）是由美國國家安全局所設計，並由美國國家標準與技術研究院所發布的。他們家族中除了 SHA-256 以外還有 SHA-224、SHA-512 等等的雜湊函式，但這裡就主要講解最常見的 SHA-256。

SHA-256 和 MD5 其實流程是差不多的，大概的流程如下：

填充資料
- 將資料的末尾添加一個"1"，為了標記填充的開始
- 添加"0"位，直到資料的長度對 512 取模後等於 448。
- 最後，將資料的原始長度（以 Bit 為單位）附加到末尾，使得填充後的資料長度為 512 的倍數。
初始化緩衝區
- SHA-256 使用八個 32 位元的變量來存儲中間和最終的雜湊值：
  - h0 = 0x6a09e667
  - h1 = 0xbb67ae85
  - h2 = 0x3c6ef372
  - h3 = 0xa54ff53a
  - h4 = 0x510e527f
  - h5 = 0x9b05688c
  - h6 = 0x1f83d9ab
  - h7 = 0x5be0cd19
- 是對自然數中前 8 個質數（2, 3, 5, 7, 11, 13, 17, 19）的平方根的小數部分取前 32 bits 而來。
處理資料
- 將填充後的資料以 512 位（64 Bytes）分成多個塊（Chunk）
- 對於每個 512 位的塊，再分為 16 個 32 位的小塊。
- 用這些 32 位的小塊和原本初始化好的 8 個變量進行迭代運算，由於過程太過於複雜，我會將其公式定義和圖解放在下面。
  $\begin{align*} &Ch(x, y, z) = (x \land y) \oplus (\neg x \land z) \\ &Maj(x, y, z) = (x \land y) \oplus (x \land z) \oplus (y \land z) \\ &\Sigma_0(x) = S^2(x) \oplus S^{13}(x) \oplus S^{22}(x) \\ &\Sigma_1(x) = S^6(x) \oplus S^{11}(x) \oplus S^{25}(x) \\ &\sigma_0(x) = S^7(x) \oplus S^{18}(x) \oplus R^3(x) \\ &\sigma_1(x) = S^{17}(x) \oplus S^{19}(x) \oplus R^{10}(x) \end{align*}$
輸出最終哈希值
- 當所有的 512 位塊都處理完成後，將 8 個變量 h0 到 h7 連接起來（大端序），形成最終的 256 位（32 字節）雜湊值。這個雜湊值即為輸入數據的 SHA-256 雜湊值。

Python Code

import hashlib

def sha256(message):
    # 將消息編碼為字節
    message_bytes = message.encode()

    # 創建 SHA-256 雜湊對象
    sha256_hash = hashlib.sha256()

    # 更新雜湊對象
    sha256_hash.update(message_bytes)

    # 獲取雜湊值
    hash_hex = sha256_hash.hexdigest()

    return hash_hex

# 測試 SHA-256 雜湊計算
message = "This is SHA-256!"
hash_result = sha256(message)
print(f"SHA-256 Value: {hash_result}")

鹽 Salt

TODO

古典密碼學 Classical Cryptography

古典密碼是指在計算機出現之前廣泛使用的密碼學技術。這些密碼技術通常基於簡單的替換或置換規則，而不涉及覆雜的數學運算。

儘管這些古典密碼在過去被廣泛使用，但它們都存在易受攻擊的缺陷，因此在現代密碼學中已經不再安全。現代密碼學使用基於覆雜數學運算和密鑰管理的加密算法來確保更高的安全性（且在現代密碼學中的觀點，他們更像是編碼而不是加密）。

以下是幾種常見的古典密碼的類型。

凱薩加密與替換式密碼 Caesar Cipher & Substitution Cipher

替換式密碼，又名取代加密法，是密碼學中按規律將文字加密的一種方式。替換式密碼中可以用不同字母數為一單元，例如每一個或兩個字母為一單元，然後再作加密。密文接收者解密時需用原加密方式解碼才可取得原文本。

簡介

凱撒密碼是一種簡單的替換密碼（Substitution cipher），通過將字母表中的每個字母向後（或向前）移動固定數量的位置來加密文本。例如，如果向後移動 3 個位置，則"A"加密為"D"，“B"加密為"E”，以此類推。

Python Code

def caesar_encrypt(plaintext, key):
    ciphertext = ""
    for char in plaintext:
        if char.isalpha():  # 只對字母進行加密
            shift = (
                65 if char.isupper() else 97
            )  # 大寫字母對應 ASCII 表中的 65，小寫字母對應 97
            encrypted_char = chr((ord(char) - shift + key) % 26 + shift)
            ciphertext += encrypted_char
        else:
            ciphertext += char  # 非字母字符保持不變
    return ciphertext


def caesar_decrypt(ciphertext, key):
    return caesar_encrypt(ciphertext, -key)  # 解密即加密的逆操作


# 示例明文和密鑰
plaintext = "This is the Caesar cipher"
key = 14

# 加密明文
encrypted_text = caesar_encrypt(plaintext, key)
print("Encrypted:", encrypted_text)

暴力破解 Brute Force

# 嘗試所有可能的密鑰進行破解
for possible_key in range(1, 26):  # 因為凱撒密碼只有 26 種可能的密鑰
    decrypted_text = caesar_decrypt(encrypted_text, possible_key)
    print(f"Key {possible_key}: {decrypted_text}")

置換密碼 Transposition Cipher

簡介

置換密碼重新排列明文中的字母，而不改變字母本身。例如，列置換密碼將明文中的字母按列排列，然後按特定規則讀取以生成密文。

維吉尼亞密碼 Vigenère Cipher

簡介

維吉尼亞密碼是一種多表替換密碼，它使用關鍵字來改變每個字母的替換規則。加密時，將明文的每個字母與關鍵字中的對應字母相結合來確定替換規則。

柵欄密碼 Rail Fence Cipher

簡介

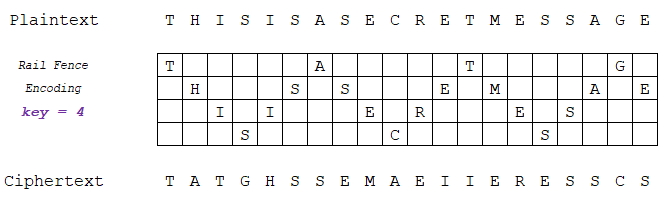
柵欄密碼將明文中的字母沿著特定的線排列，然後以不同的方式讀取以生成密文。例如，3 欄柵欄密碼將字母交替排列成三行，然後以從上到下、從左到右的順序讀取。以下是圖例。

前言

為甚麼會想寫這篇文

柯克霍夫原則 Kerckhoffs’s principle

領域展開：密碼學的三大領域

編碼 Encoding

雜湊 Hashing

加密 Encryption

常見編碼 Common Encoding

ASCII Encoding

簡介

Python Code

Base64 Encoding

簡介

原理

Python Code

延伸

URL Encoding

簡介

Python Code

小結

常見雜湊函式 Common Hash Functions

MD5

簡介

端序 Endian

Python Code

MD5 已死

SHA-256

簡介

Python Code

鹽 Salt

古典密碼學 Classical Cryptography

凱薩加密與替換式密碼 Caesar Cipher & Substitution Cipher

簡介

Python Code

暴力破解 Brute Force

置換密碼 Transposition Cipher

簡介

維吉尼亞密碼 Vigenère Cipher

簡介

柵欄密碼 Rail Fence Cipher

簡介

對稱式加密 Symmetric Cryptography

非對稱式加密 Asymmetric Cryptography

RSA

RSA 介紹

小公鑰指數攻擊（Low public exponent attack）

Coppersmith’s Attack

題目

CX330