All-in-One PicoCTF Writeups: Crypto

All-in-One PicoCTF Writeups: Crypto
CX330前言
其實好像也沒什麼好講前言的,但就是不想要一開始就是題目分類,所以還是放了個前言 XD。
自己在刷 PicoCTF 的時候常常發現,幾乎所有的 writeup 都是英文的居多,所以想說來寫個完整一點的中文版!總之呢這裡就是會盡量彙整所有的 picoCTF 的題目在這邊(但是因為已經寫了 60 題左右才開始打算來寫 writeup,所以可能前面的部分會等其他都寫完再來補),如果有需要就可以直接來這邊看所有的 writeup,就這樣啦!希望能幫忙到你。
Easy1
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
+----------------------------------------------------
A | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B | B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C | C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D | D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E | E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F | F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G | G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H | H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I | I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J | J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K | K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L | L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M | M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N | N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O | O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P | P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q | Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R | R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S | S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T | T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U | U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V | V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W | W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X | X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y | Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z | Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
Cipher: UFJKXQZQUNB
Key: SOLVECRYPTO這題是一個維吉尼亞密碼。維吉尼亞密碼(法語:Chiffre de Vigenère,又譯維熱納爾密碼)是使用一系列凱撒密碼組成密碼字母表的加密算法,屬於多表密碼的一種簡單形式。維基百科
解密的方式也很簡單,最上面一列是明文,最左邊那行是 KEY,這樣對應起來中間的字元就是密文。知道了這個之後回推回去就可以得到明文。
cipher = "UFJKXQZQUNB"
key = "SOLVECRYPTO"
pt = ""
for i in range(len(cipher)):
shift = ord(key[i]) - 65 # 獲取密鑰字母的偏移量
c = ord(cipher[i]) # 獲取密文當中目前的字母
c = (c - shift - 65) % 26 + 65 # 用偏移量進行解密
pt += chr(c)
print(f"Message: {pt}")而最後的 flag 如下
picoCTF{CRYPTOISFUN}Caesar
如同題目所說,這題就是個基本的凱薩加密。題目給了加密過的 flag
picoCTF{gvswwmrkxlivyfmgsrhnrisegl}就把裡面那串拿去解密,因為不知道偏移量是多少,所以就暴力破解。
cipher = "gvswwmrkxlivyfmgsrhnrisegl"
def caesar_cipher(text, shift):
plaintext = ""
for c in text:
plaintext += chr((ord(c) - 97 + shift) % 26 + 97)
return plaintext
for i in range(26):
plaintext = caesar_cipher(cipher, i)
print(f"Shift {i}: {plaintext}")跑出來的結果中,看起來是 crossingtherubicondjneoach最合理,所以這就是 flag 了
picoCTF{crossingtherubicondjneoach}New Caesar
題目給了一個密文和一個 Python 腳本。
apbopjbobpnjpjnmnnnmnlnbamnpnononpnaaaamnlnkapndnkncamnpapncnbannaapncndnlnpnaimport string
LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]
def b16_encode(plain):
enc = ""
for c in plain:
binary = "{0:08b}".format(ord(c))
enc += ALPHABET[int(binary[:4], 2)]
enc += ALPHABET[int(binary[4:], 2)]
return enc
def shift(c, k):
t1 = ord(c) - LOWERCASE_OFFSET
t2 = ord(k) - LOWERCASE_OFFSET
return ALPHABET[(t1 + t2) % len(ALPHABET)]
flag = "redacted"
key = "redacted"
assert all([k in ALPHABET for k in key])
assert len(key) == 1
b16 = b16_encode(flag)
enc = ""
for i, c in enumerate(b16):
enc += shift(c, key[i % len(key)])
print(enc)先觀察這個加密腳本。發現他是把明文每個字母的 Ascii 值轉為 Binary 後,從左邊補 0 補到 8 個 Bits,然後每 4 位元分為一塊,每塊的二進制數字(0 ~ 15)映射到 Base16 的字符集(a ~ p)。再把這個東西拿去做 shift,就是凱薩加密的變形。
總之解密的話就是反著來,就不詳細解釋了。Exploit 如下:
import string
LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]
def b16_encode(plain):
enc = ""
for c in plain:
binary = "{0:08b}".format(ord(c))
enc += ALPHABET[int(binary[:4], 2)] # Since 4 bits can represent 16 characters
enc += ALPHABET[int(binary[4:], 2)]
return enc
def b16_decode(b16):
dec = ""
for c in range(0, len(b16), 2):
first = b16[c]
second = b16[c + 1]
first_index = ALPHABET.index(first)
second_index = ALPHABET.index(second)
binary = bin(first_index)[2:].zfill(4) + bin(second_index)[2:].zfill(4)
dec += chr(int(binary, 2))
return dec
def shift(c, k):
t1 = ord(c) - LOWERCASE_OFFSET # (c - 97 + k - 97) % 16 = result
t2 = ord(k) - LOWERCASE_OFFSET
return ALPHABET[(t1 + t2) % len(ALPHABET)] # two numbers sum modulo 16
def inverse_shift(c, k):
t1 = ord(c) - LOWERCASE_OFFSET
t2 = ord(k) - LOWERCASE_OFFSET
return ALPHABET[(t1 - t2) % len(ALPHABET)] # two numbers difference modulo 16
enc = "apbopjbobpnjpjnmnnnmnlnbamnpnononpnaaaamnlnkapndnkncamnpapncnbannaapncndnlnpna"
for key in ALPHABET:
dec = ""
for i, c in enumerate(enc):
dec += inverse_shift(c, key[i % len(key)])
b16_dec = b16_decode(dec)
print(f"Decrypted flag: {b16_dec}")暴力破解後,看起來最像 Flag 的就是 et_tu?_23217b54456fb10e908b5e87c6e89156這個了。最後自己幫它包上 picoCTF{}提交,果然是正確的。
picoCTF{et_tu?_23217b54456fb10e908b5e87c6e89156}rotation
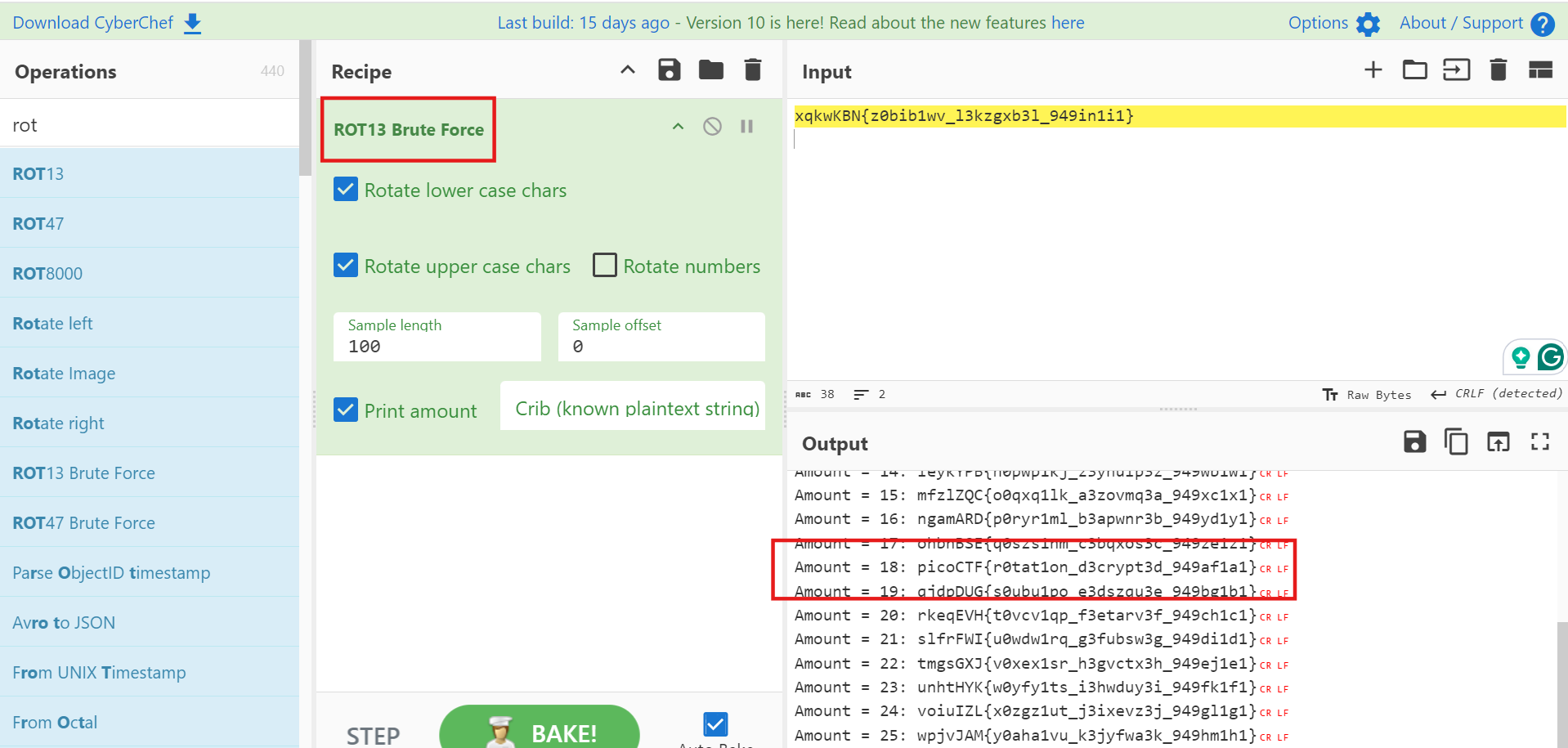
這題給了一個加密後的密文。
xqkwKBN{z0bib1wv_l3kzgxb3l_949in1i1}看起來就是 Transposition Cipher,直接拿去網路上那種凱薩密碼暴力破解。這邊使用CyberChef。
picoCTF{r0tat1on_d3crypt3d_949af1a1}Mind your Ps and Qs
這題是個 RSA 加密,先來複習一下 RSA 加密裡面的流程和參數。
複習完後,看一下題目的說明。
Description:
In RSA, a small e value can be problematic, but what about N? Can you decrypt this?
==============================
Decrypt my super sick RSA:
c: 421345306292040663864066688931456845278496274597031632020995583473619804626233684
n: 631371953793368771804570727896887140714495090919073481680274581226742748040342637
e: 65537這題的敘述中告訴我們,當 e 太小的時候我們可以使用小公鑰指數攻擊(Low public exponent attack),而題目要我們思考當 N 太小的時候我們可以如何利用。
回去看一下 RSA 加密的流程後,我們發現 N 是兩個質數的乘積,而當 N 太小的時候我們就可以暴力破解出兩個 P 跟 Q。這裡我們直接使用 FactorDB 去找 N 的因數,就可以找到 P 和 Q 了。
而有了 P 和 Q,我們就可以順著 RSA 流程找到明文 M 了,我寫了個 Python 幫我找出明文,如下
from Crypto.Util.number import inverse, long_to_bytes
from factordb.factordb import FactorDB
def long2str(long_int: int) -> str:
return long_to_bytes(long_int).decode()
c = 421345306292040663864066688931456845278496274597031632020995583473619804626233684
n = 631371953793368771804570727896887140714495090919073481680274581226742748040342637
e = 65537
# From Factor db find p and q
f = FactorDB(n)
f.connect()
factors = f.get_factor_list()
p = factors[0]
q = factors[1]
phi_n = (p - 1) * (q - 1)
d = inverse(e, phi_n)
print(f"Private key: d = {d}")
m = pow(c, d, n)
print(f"Decrypted message: m = {long2str(m)}")最後找到的明文會是一個很大的數字,這時候再用 Crypto.Util.number 的 long_to_bytes 並 decode,將其轉為字符串,就可以得到 flag 了。
picoCTF{sma11_N_n0_g0od_55304594}No padding, no problem
可以先看過這篇 Day 14:[離散數學]同餘(Mod)是什麼?
當我們把題目給的密文拿去解密,他會說 Will not decrypt the ciphertext. Try Again。代表題目的這支程式應該是在偵測我們輸入的是否為 Ciphertext。而我們知道
所以我們利用題目給的 c 和 n 相加後,輸入到他的程式會得到:
Here you go: 290275030195850039473456618367455885069965748851278076756743720446703314517401359267322769037469251445384426639837648598397接著只要再利用 Crypto 的 long_to_bytes3 方法就可以找到明文,如下:
from Crypto.Util.number import long_to_bytes
from pwn import *
r = remote("mercury.picoctf.net", 10333)
r.recvuntil("n:")
n = int(r.recvline().strip())
r.recvuntil("ciphertext:")
c = int(r.recvline().strip())
num = n + c
r.sendline(str(num))
r.recvuntil("Here you go:")
m = int(r.recvline().strip())
r.close()
print(long_to_bytes(m))picoCTF{m4yb3_Th0se_m3s54g3s_4r3_difurrent_1772735}interencdec
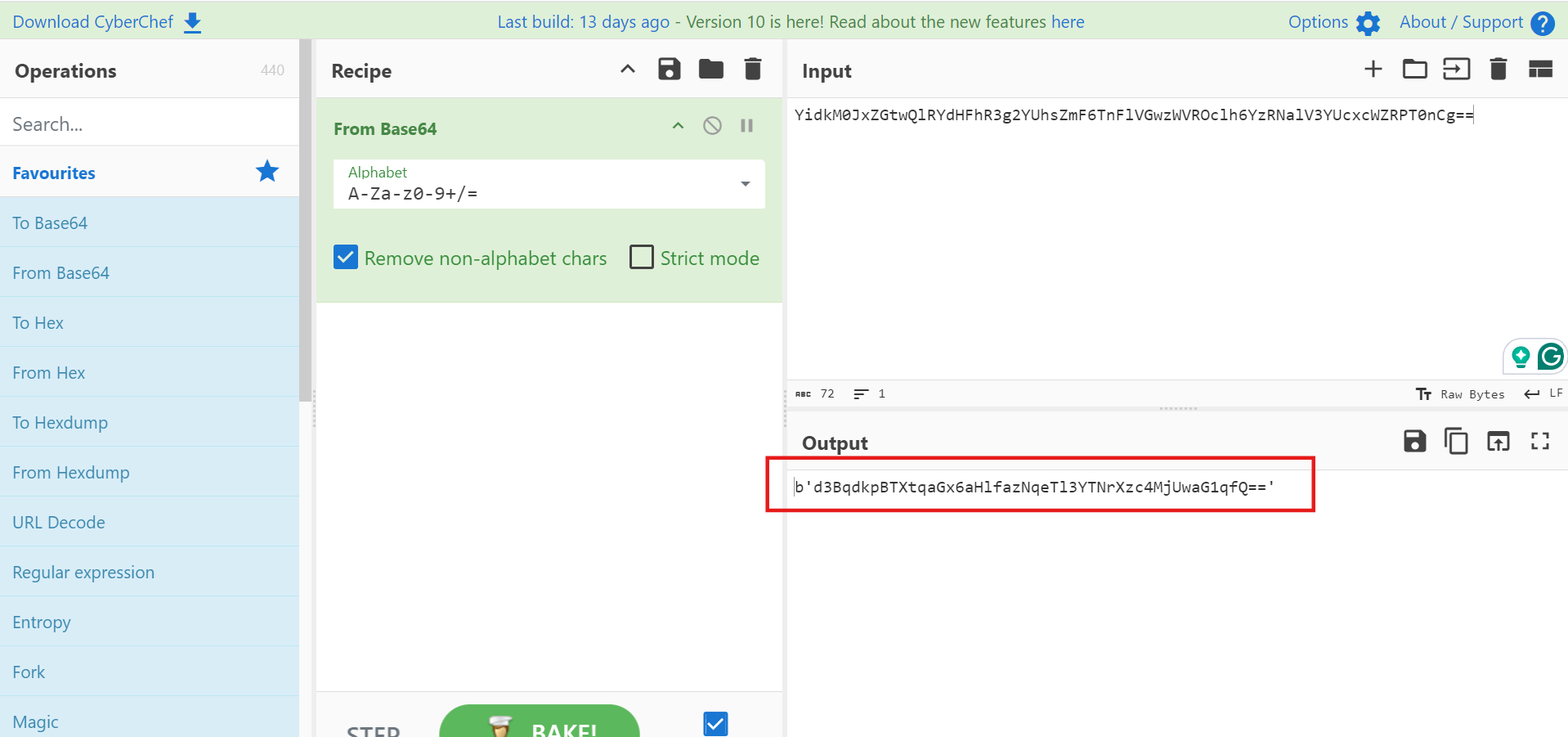
題目給了密文 enc_flag,如下。
YidkM0JxZGtwQlRYdHFhR3g2YUhsZmF6TnFlVGwzWVROclh6YzRNalV3YUcxcWZRPT0nCg==因為他最後面的兩個 ==讓他看起來很像是 base64 的格式,所以就用 base64 先 Decode 一下。這邊用的是CyberChef這款工具,他可以線上進行很多種的編碼解碼、加密等等。
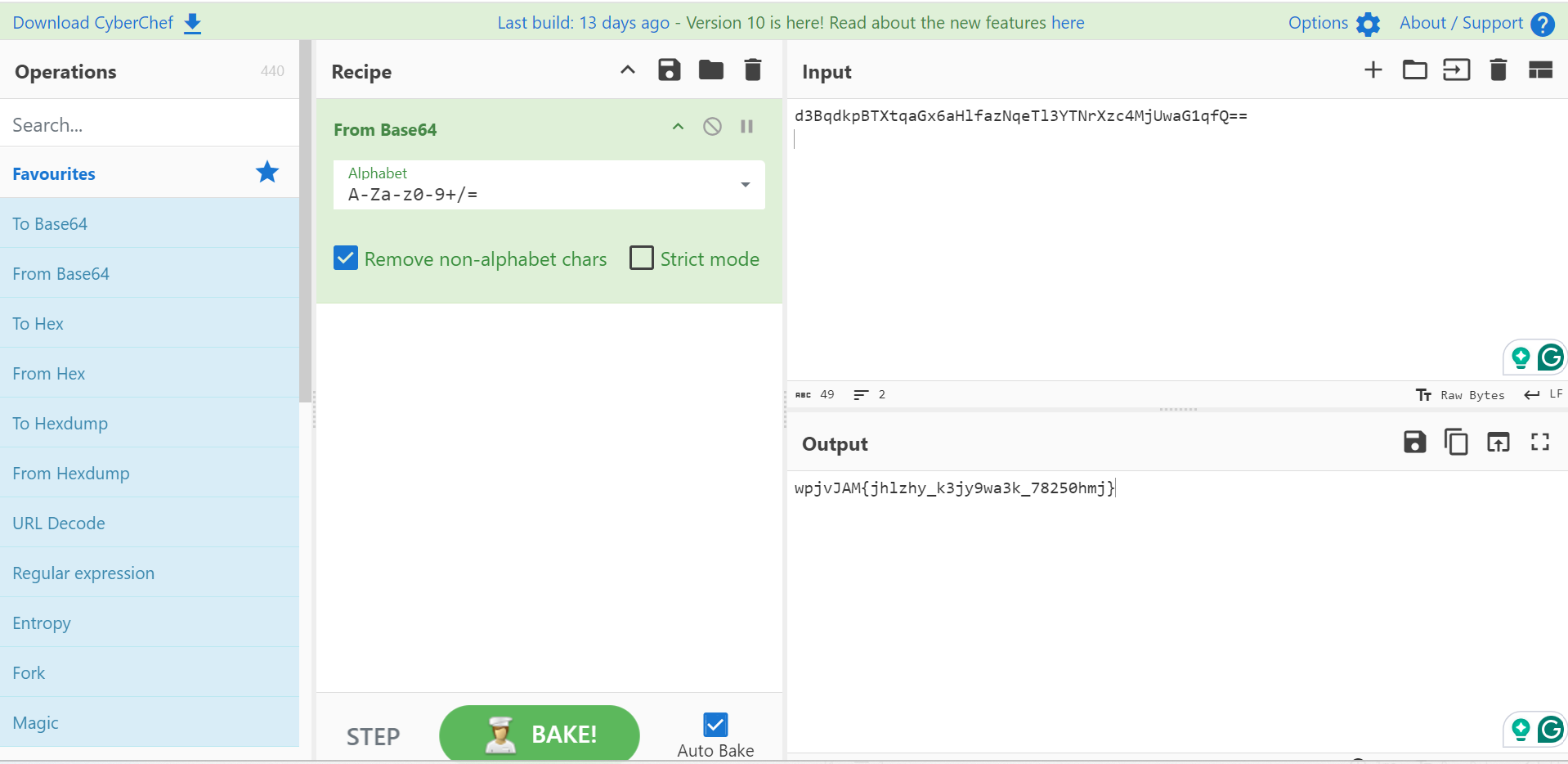
d3BqdkpBTXtqaGx6aHlfazNqeTl3YTNrXzc4MjUwaG1qfQ==解碼一次後長這樣,還是很像 base64 的格式,所以我又做了一次 base64 解碼。(注意:這邊要把前面的 b 拿掉,只留引號中的內容)
wpjvJAM{jhlzhy_k3jy9wa3k_78250hmj}再解碼一次後變成了這樣的形狀,看起來已經有 Flag 的雛型了(因為大括號),所以猜測它是某種置換密碼。就用最普遍的凱薩密碼來暴力解解看吧!Exploit 如下:
enc_flag = input("Enter the encrypted flag: ")
for i in range(1, 27):
dec_flag = ""
for char in enc_flag:
if char.isalpha():
if char.isupper():
dec_flag += chr((ord(char) - ord("A") - i) % 26 + ord("A"))
else:
dec_flag += chr((ord(char) - ord("a") - i) % 26 + ord("a"))
else:
dec_flag += char
if "pico" in dec_flag.lower():
print(dec_flag)picoCTF{caesar_d3cr9pt3d_78250afc}Easy peasy
想了解 OTP 可以去看看這個 一次性密碼本
先看題目。
******************Welcome to our OTP implementation!******************
This is the encrypted flag!
551e6c4c5e55644b56566d1b5100153d4004026a4b52066b4a5556383d4b0007
What data would you like to encrypt?在這題中,我們要先閱讀他給我們的 Code。在 encrypt 函式中我們可以看到一些事情。因為題目給的 Cipher 的長度為 64,又因為他是以十六進制的方式輸出 Cipher,所以我們可以知道他用掉的 key_location長度為 32,也就是說,我們下次在加密的時候是用第 33 位開始的 key。
def encrypt(key_location):
ui = input("What data would you like to encrypt? ").rstrip()
if len(ui) == 0 or len(ui) > KEY_LEN:
return -1
start = key_location # 這裡從32開始
stop = key_location + len(ui)
kf = open(KEY_FILE, "rb").read()
if stop >= KEY_LEN:
stop = stop % KEY_LEN
key = kf[start:] + kf[:stop]
else:
key = kf[start:stop]
key_location = stop
result = list(map(lambda p, k: "{:02x}".format(ord(p) ^ k), ui, key))
print("Here ya go!\n{}\n".format("".join(result)))
return key_location知道了我們第一次輸入要加密的銘文是從第 32 個 key 開始後,我們要想辦法可以使用到跟題目一樣的那組 key,而在程式碼的這個區段我們可以發現一些事。
if stop >= KEY_LEN:
stop = stop % KEY_LEN
key = kf[start:] + kf[:stop]在這邊,如果我們讓 stop和 KEY_LEN相等,讓 stop % KEY_LEN == 0的話,stop就會被設定為 0,所以我們就可以讓 one-time pad 被重複使用了!所以我們先輸入一堆沒用的字元去填充那個區間段,讓他把第一個 50000 循環結束,再進入一次循環後我們就可以得到跟題目一樣的 key 了。
然後因為他加密的方法是用計算 XOR 的方式,所以我們可以簡單地透過再計算一次 XOR 得到明文,如下:
key \oplus pt = ct$$ $$key \oplus ct = pt$$ $$pt \oplus ct = key
from pwn import *
import binascii # binascii.unhexlify() is used to convert hex to binary
offset = 50000 - 32
r = remote("mercury.picoctf.net", 11188)
print(r.recvline())
print(r.recvline())
encrypted_flag = r.recvline().strip()
print(encrypted_flag)
r.recvuntil(b"?")
r.sendline(b"A" * offset)
r.recvuntil(b"?")
r.sendline(b"A" * 32)
r.recvline()
encoded = r.recvline().strip()
encoded = binascii.unhexlify(encoded)
message = "A" * 32
key = []
for i in range(len(encoded)):
key.append(ord(message[i]) ^ encoded[i])
flag = []
encrypted_flag = binascii.unhexlify(encrypted_flag)
for i in range(len(encrypted_flag)):
flag.append(chr(key[i] ^ encrypted_flag[i]))
flag = "".join(flag)
print(flag)Custom encryption
這題給了兩個檔案。一個是加密後的 flag,裡面還包含了加密需要的一些變量;另一個是加密腳本。既然給了腳本,那就先來看看 Code 吧。我結合了題目給的加密後的 flag 的資訊,把註解直接寫在了代碼裡面,看看吧!
from random import randint
import sys
def generator(g, x, p):
return pow(g, x) % p
# 密文 = 明文的每個字元ASCII碼 * 密鑰 * 311並append到一個list
def encrypt(plaintext, key):
cipher = []
for char in plaintext:
cipher.append(((ord(char) * key * 311)))
return cipher
def is_prime(p):
v = 0
for i in range(2, p + 1):
if p % i == 0:
v = v + 1
if v > 1:
return False
else:
return True
def dynamic_xor_encrypt(plaintext, text_key):
cipher_text = ""
key_length = len(text_key)
for i, char in enumerate(plaintext[::-1]): # 從明文的末尾開始
key_char = text_key[i % key_length] # 循環text_key裡面每個字元
encrypted_char = chr(ord(char) ^ ord(key_char)) # 對應的密文 = 明文 ^ 密鑰
cipher_text += encrypted_char
return cipher_text
def test(plain_text, text_key):
p = 97
g = 31
if not is_prime(p) and not is_prime(g):
print("Enter prime numbers")
return
a = randint(p - 10, p)
b = randint(g - 10, g)
print(f"a = {a}")
print(f"b = {b}")
# a = 89
# b = 27
# p = 97
# g = 31
u = generator(g, a, p) # u = 31 ** 89 % 97 = 49
v = generator(g, b, p) # u = 31** 27 % 97 = 85
key = generator(v, a, p) # key = 85 ** 89 % 97 = 12
b_key = generator(u, b, p) # b_key = 49 ** 27 % 97 = 12
shared_key = None
if key == b_key:
shared_key = key # shared_key = 12
else:
print("Invalid key")
return
semi_cipher = dynamic_xor_encrypt(plain_text, text_key)
cipher = encrypt(semi_cipher, shared_key)
print(f"cipher is: {cipher}")
if __name__ == "__main__":
message = sys.argv[1]
test(message, "trudeau")由上面的代碼可以知道,它是經過了兩次的加密,一次是把明文反過來並讓其對 text_key循環做 XOR,第二次是把第一次加密得到的東西轉 ASCII 並乘以 key 再乘以 311。
解密的話就反過來,先去除以 311 再除以 key(這裡為 12),得到一個半密文(semi_cipher)。接下來這個半密文要先反轉,再用它寫好的 function 去做 XOR(因為它的 function 裡面又有一次反轉,所以這樣剛好會是和加密時相同的順序),最後得到的這個明文還要再反轉一次,才會得到正確的 flag。至於為甚麼要反轉兩次,解釋如下:
假設題目的dynamic_xor_encrypt為f,明文為ABC
加密:
f(ABC, KEY) = C'B'A'
解密:
第一次反轉,把C'B'A變為A'B'C,所以在f裡就會計算C'B'A對KEY的XOR
f(A'B'C, KEY) = CBA
第二次反轉,把CBA轉為ABC
flag = ABC希望這樣解釋有比較清楚一點!總之照這樣解密就可以得到 flag 啦,以下是我的解密的代碼:
def decrypt(cipher: list, key: int, text_key: str) -> str:
semi_cipher = ""
for encrypted_value in cipher:
decrypted_value = encrypted_value // (key * 311) # 使用 // 返回int
semi_cipher += chr(decrypted_value)
semi_cipher = semi_cipher[::-1] # 將密文反轉
plaintext = dynamic_xor_encrypt(semi_cipher, text_key)
return plaintext
cipher = [
33588,
276168,
261240,
302292,
343344,
328416,
242580,
85836,
82104,
156744,
0,
309756,
78372,
18660,
253776,
0,
82104,
320952,
3732,
231384,
89568,
100764,
22392,
22392,
63444,
22392,
97032,
190332,
119424,
182868,
97032,
26124,
44784,
63444,
]
plaintext = decrypt(cipher, 12, "trudeau") # since we know the key is 12
print(f"plaintext is: {plaintext[::-1]}")picoCTF{custom_d2cr0pt6d_dc499538}Mini RSA
題目給了一組 RSA 加密的密文,還有公鑰(n, e),如下。
N: 1615765684321463054078226051959887884233678317734892901740763321135213636796075462401950274602405095138589898087428337758445013281488966866073355710771864671726991918706558071231266976427184673800225254531695928541272546385146495736420261815693810544589811104967829354461491178200126099661909654163542661541699404839644035177445092988952614918424317082380174383819025585076206641993479326576180793544321194357018916215113009742654408597083724508169216182008449693917227497813165444372201517541788989925461711067825681947947471001390843774746442699739386923285801022685451221261010798837646928092277556198145662924691803032880040492762442561497760689933601781401617086600593482127465655390841361154025890679757514060456103104199255917164678161972735858939464790960448345988941481499050248673128656508055285037090026439683847266536283160142071643015434813473463469733112182328678706702116054036618277506997666534567846763938692335069955755244438415377933440029498378955355877502743215305768814857864433151287
e: 3
ciphertext (c): 1220012318588871886132524757898884422174534558055593713309088304910273991073554732659977133980685370899257850121970812405700793710546674062154237544840177616746805668666317481140872605653768484867292138139949076102907399831998827567645230986345455915692863094364797526497302082734955903755050638155202890599808147130204332030239454609548193370732857240300019596815816006860639254992255194738107991811397196500685989396810773222940007523267032630601449381770324467476670441511297695830038371195786166055669921467988355155696963689199852044947912413082022187178952733134865103084455914904057821890898745653261258346107276390058792338949223415878232277034434046142510780902482500716765933896331360282637705554071922268580430157241598567522324772752885039646885713317810775113741411461898837845999905524246804112266440620557624165618470709586812253893125417659761396612984740891016230905299327084673080946823376058367658665796414168107502482827882764000030048859751949099453053128663379477059252309685864790106不難發現,這題的公鑰指數 e 超小,只有 3。所以我們使用小公鑰指數攻擊(Coppersmith’s attack, Low public exponent attack)。由於題目有說略大於,故其解題原理如下(為密文,為明文,是公鑰指數,是公鑰模數):
為了計算明文,我寫了一個 Python 腳本,如下。
import gmpy2
from Crypto.Util.number import long_to_bytes
# 宣告題目所給的n, e, c
n = 1615765684321463054078226051959887884233678317734892901740763321135213636796075462401950274602405095138589898087428337758445013281488966866073355710771864671726991918706558071231266976427184673800225254531695928541272546385146495736420261815693810544589811104967829354461491178200126099661909654163542661541699404839644035177445092988952614918424317082380174383819025585076206641993479326576180793544321194357018916215113009742654408597083724508169216182008449693917227497813165444372201517541788989925461711067825681947947471001390843774746442699739386923285801022685451221261010798837646928092277556198145662924691803032880040492762442561497760689933601781401617086600593482127465655390841361154025890679757514060456103104199255917164678161972735858939464790960448345988941481499050248673128656508055285037090026439683847266536283160142071643015434813473463469733112182328678706702116054036618277506997666534567846763938692335069955755244438415377933440029498378955355877502743215305768814857864433151287
e = 3
c = 1220012318588871886132524757898884422174534558055593713309088304910273991073554732659977133980685370899257850121970812405700793710546674062154237544840177616746805668666317481140872605653768484867292138139949076102907399831998827567645230986345455915692863094364797526497302082734955903755050638155202890599808147130204332030239454609548193370732857240300019596815816006860639254992255194738107991811397196500685989396810773222940007523267032630601449381770324467476670441511297695830038371195786166055669921467988355155696963689199852044947912413082022187178952733134865103084455914904057821890898745653261258346107276390058792338949223415878232277034434046142510780902482500716765933896331360282637705554071922268580430157241598567522324772752885039646885713317810775113741411461898837845999905524246804112266440620557624165618470709586812253893125417659761396612984740891016230905299327084673080946823376058367658665796414168107502482827882764000030048859751949099453053128663379477059252309685864790106
# 暴力破解 k * n + c 的 e 次方根
k = 0
while True:
m, is_root = gmpy2.iroot(k * n + c, e)
if is_root:
break
else:
k += 1
# 數字轉字串
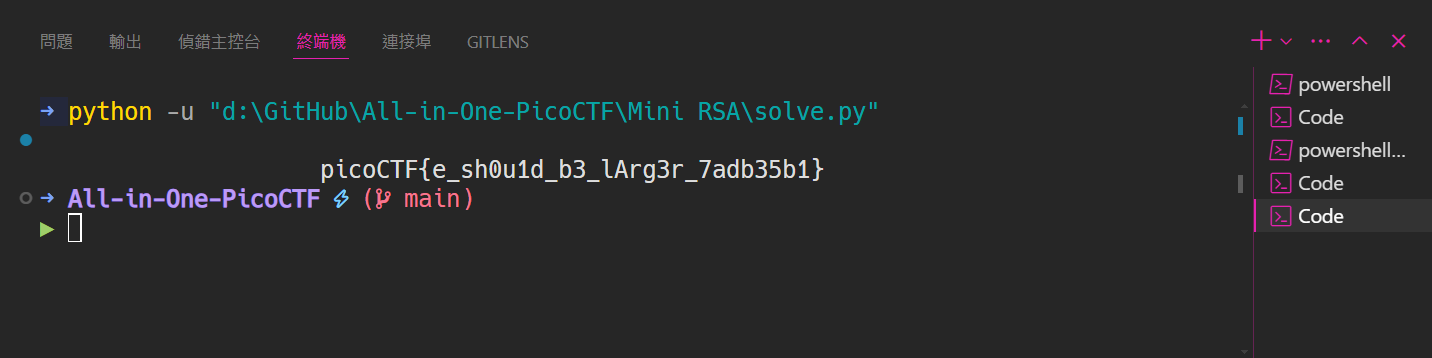
print(long_to_bytes(m).decode())執行後就可以找到 flag 啦~
picoCTF{e_sh0u1d_b3_lArg3r_7adb35b1}miniRSA
這題的原理和上面那題一模一樣,都是 e 太小所以用小公鑰指數攻擊。想知道更詳細原理看上面那題,這邊直接上 Exploit。
import gmpy2
from Crypto.Util.number import long_to_bytes
# 宣告題目所給的n, e, c
n = 29331922499794985782735976045591164936683059380558950386560160105740343201513369939006307531165922708949619162698623675349030430859547825708994708321803705309459438099340427770580064400911431856656901982789948285309956111848686906152664473350940486507451771223435835260168971210087470894448460745593956840586530527915802541450092946574694809584880896601317519794442862977471129319781313161842056501715040555964011899589002863730868679527184420789010551475067862907739054966183120621407246398518098981106431219207697870293412176440482900183550467375190239898455201170831410460483829448603477361305838743852756938687673
e = 3
c = 2205316413931134031074603746928247799030155221252519872650080519263755075355825243327515211479747536697517688468095325517209911688684309894900992899707504087647575997847717180766377832435022794675332132906451858990782325436498952049751141
# 暴力破解 k * n + c 的 e 次方根
k = 0
while True:
m, is_root = gmpy2.iroot(k * n + c, e)
if is_root:
break
else:
k += 1
# 數字轉字串
print(long_to_bytes(m).decode())picoCTF{n33d_a_lArg3r_e_d0cd6eae}b00tl3gRSA2
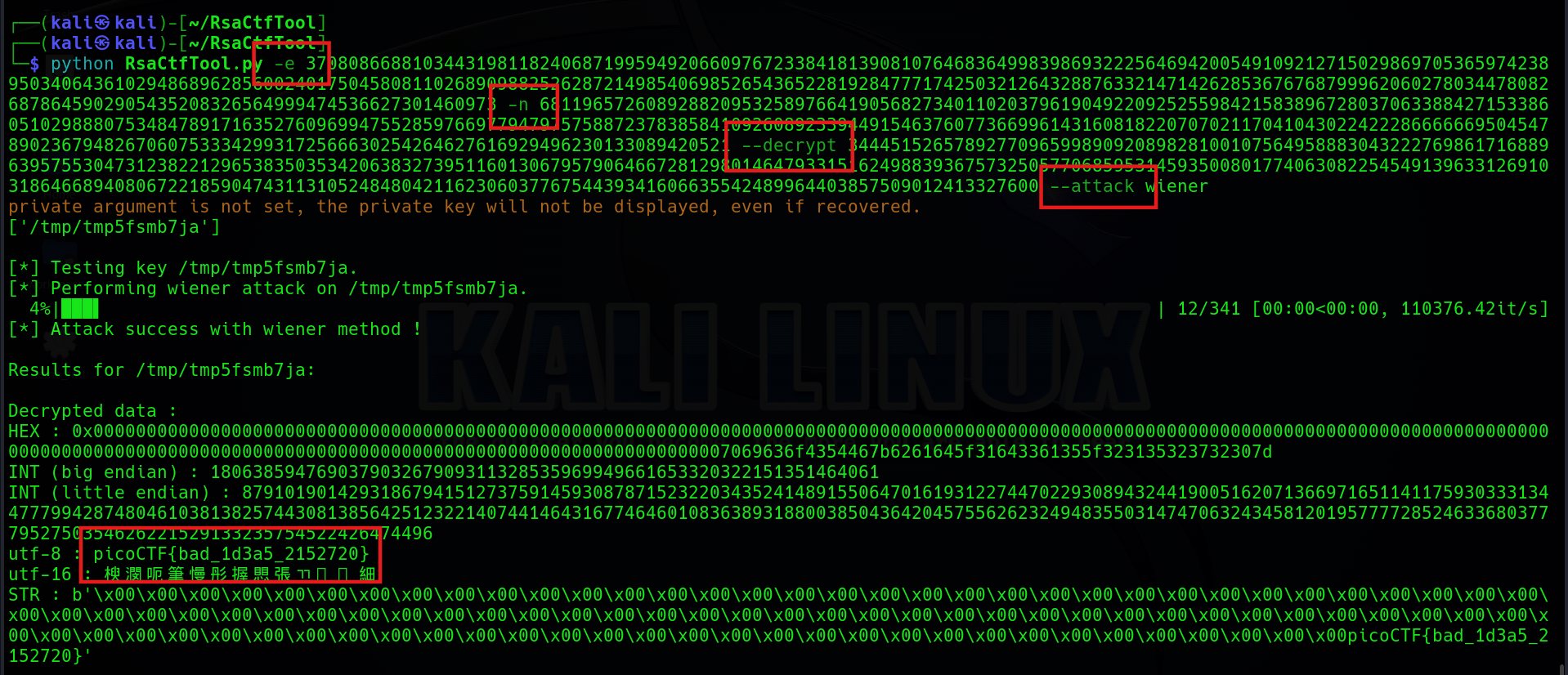
這題給了一個 Netcat 連接方式 nc jupiter.challenges.picoctf.org 57464。先連進去主機看看吧。連進去後可以得到公鑰(e, n)跟密文 C。
c: 34445152657892770965998909208982810010756495888304322276986171688963957553047312382212965383503534206383273951160130679579064667281298014647933151624988393675732505770685953145935008017740630822545491396331269103186466894080672218590474311310524848042116230603776754439341606635542489964403857509012413327600
n: 68119657260892882095325897664190568273401102037961904922092525598421583896728037063388427153386051029888075348478917163527609699475528597669779479757588723783858410926089233944915463760773669961431608182207070211704104302242228666666950454789023679482670607533342993172566630254264627616929496230133089420521
e: 37080866881034431981182406871995949206609767233841813908107646836499839869322256469420054910921271502986970536597423895034064361029486896285600240175045808110268909882526287214985406985265436522819284777174250321264328876332147142628536767687999620602780344780826878645902905435208326564999474536627301460973在題目的描述中他說:
In RSA d is a lot bigger than e, why don’t we use d to encrypt instead of e?
意思是在這題裡面他把 和 互換了,用 來加密 。下面這篇文章有詳細說了為甚麼不應該使用這種做法。
簡而言之,當私鑰指數()比較小的時候,可以使用Wiener’s attack。這邊可以使用一個開源工具來幫助我們快速執行攻擊。
使用方式請查看官方文檔。總之 Exploit 如下。
python RsaCtfTool.py -e 37080866881034431981182406871995949206609767233841813908107646836499839869322256469420054910921271502986970536597423895034064361029486896285600240175045808110268909882526287214985406985265436522819284777174250321264328876332147142628536767687999620602780344780826878645902905435208326564999474536627301460973 -n 68119657260892882095325897664190568273401102037961904922092525598421583896728037063388427153386051029888075348478917163527609699475528597669779479757588723783858410926089233944915463760773669961431608182207070211704104302242228666666950454789023679482670607533342993172566630254264627616929496230133089420521 --decrypt 34445152657892770965998909208982810010756495888304322276986171688963957553047312382212965383503534206383273951160130679579064667281298014647933151624988393675732505770685953145935008017740630822545491396331269103186466894080672218590474311310524848042116230603776754439341606635542489964403857509012413327600 --attack wiener總之就是把參數都設定好,就可以成功得到 Flag 了。
picoCTF{bad_1d3a5_2152720}b00tl3gRSA3
這題和上一題一樣,先用 Netcat 連線到主機,得到資訊如下。
c: 1155413374658603081887942538070618568058048531029758454280998255793925425541835159695263849863790503010031220771999047690488595295467625987010931696477313386062384452816188902386984531395080585643524053777943484599038478398898775019494628236550977835910935567524611329303821647514235510296512723444159728500460371101677191814101634547011569775
n: 3009815969095519381043948515174929441467634594821498333858615496361783804562611599728570248270874306617036697889577813844217713194056663725350522605669349001546826005570895246471872723077264759401472551915667965016802426155245585986786567513487278588996436597960321248870612409759311004096684257474660765774013406405351078796165091907796029759
e: 65537題目說了
Why use p and q when I can use more?
意思是,這題的初始質數不只有 和 。所以我們只要找到歐拉函數 ,並且正常走流程就可以了。由於他不只有 和 兩個質數,分解起來會容易很多。Exploit 如下。
from sympy.ntheory import factorint
from Crypto.Util.number import long_to_bytes
def get_phi(n):
f = factorint(n) # 返回一個字典,key為質因數,value為該質因數的冪
phi = 1
for a, b in f.items():
phi *= pow(a, b - 1) * (a - 1)
return phi
# 宣告題目給的資訊
c = 1155413374658603081887942538070618568058048531029758454280998255793925425541835159695263849863790503010031220771999047690488595295467625987010931696477313386062384452816188902386984531395080585643524053777943484599038478398898775019494628236550977835910935567524611329303821647514235510296512723444159728500460371101677191814101634547011569775
n = 3009815969095519381043948515174929441467634594821498333858615496361783804562611599728570248270874306617036697889577813844217713194056663725350522605669349001546826005570895246471872723077264759401472551915667965016802426155245585986786567513487278588996436597960321248870612409759311004096684257474660765774013406405351078796165091907796029759
e = 65537
phi = get_phi(n)
d = pow(e, -1, phi)
m = pow(c, d, n)
print(long_to_bytes(m))這邊的 get_phi(n)是用到了以下的求歐拉函數的公式:
這樣求出來 後就可以用正常計算流程找到明文 了。
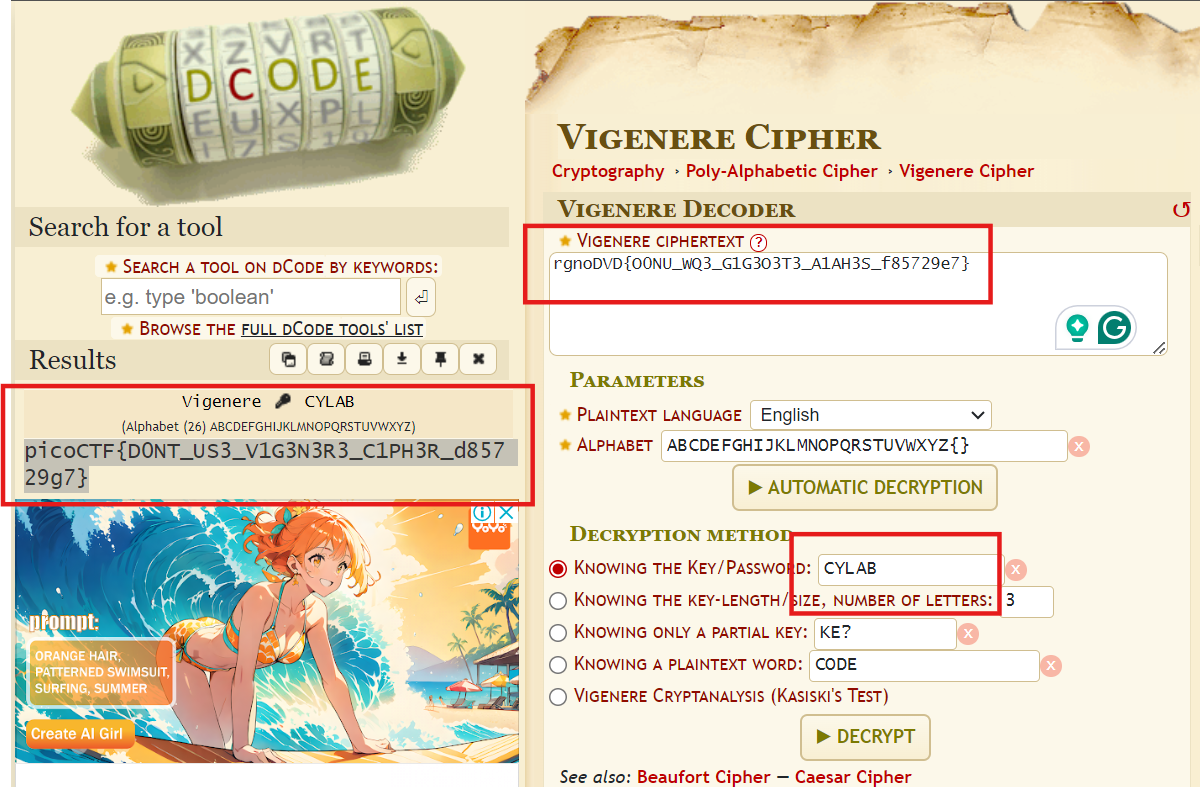
picoCTF{too_many_fact0rs_8606199}Vigenere
這題給了一個加密後的密文跟 Key,然後題目也告訴我們是 Vigenere Cipher,直接拿去 Online decoder 解就行。(我也不知道為甚麼他難度是 Medium LMAO)
picoCTF{D0NT_US3_V1G3N3R3_C1PH3R_d85729g7}Pixelated
這題給了兩張圖片,並且是一個叫做 Visual Cryptography 的東西。題目圖片如下。
這邊我用 Stegsolve 去 Combine 兩張圖片。先打開第一張圖片後點選 Analyze > Image Combiner,再點選第二張圖片。之後它會跳出一個介面讓你選擇 Combine 的方式,預設是 XOR,一直點向右的箭頭直到方法變成 ADD 的時候就可以看到 Flag 啦。
picoCTF{d562333d}解完後我有看了一下其他人的 Writeups,我發現有人是用 Python 解的覺得很酷,附上來給大家看看。(Writeup)
# import Image
from PIL import Image
# open both photos
i1 = Image.open('scrambled1.png')
i2 = Image.open('scrambled2.png')
# get width and height
width1, height1 = i1.size
# open new image
i3 = Image.new('RGB', (width1, height1))
# load the pixels
pixels = i3.load()
# loop through all pixels
for i in range(width1):
for j in range(height1):
# xor the values
x = i1.getpixel((i,j))[0] ^ i2.getpixel((i,j))[0]
y = i1.getpixel((i,j))[1] ^ i2.getpixel((i,j))[1]
z = i1.getpixel((i,j))[2] ^ i2.getpixel((i,j))[2]
# if all white then convert to black
if (x,y,z) == (255,255,255):
(x,y,z) = (0,0,0)
# put the new pixels in place
i3.putpixel((i,j), (x,y,z))
# save the image
i3.save("test.png", "PNG")HideToSee
這題給了一個圖片,圖片上寫的字說這是一個 Atbash Cipher,查了一下,就是一種把字母順序反過來的 Substitution Cipher。提示有說要 Extract it,所以猜測是用 Steghide,這邊先把資料提取出來。
steghide extract -sf atbash.jpg這會提取出一個encrypted.txt文件,看一下內容。
krxlXGU{zgyzhs_xizxp_8z0uvwwx}直接把這個拿去網路上的解密工具,Flag 就出來了。
picoCTF{atbash_crack_8a0feddc}college-rowing-team
這題給了一個加密腳本和一個密文(含公鑰),先來看看加密腳本encrypt.py。
#!/usr/bin/env python3
import random
from Crypto.Util.number import getPrime, bytes_to_long
with open("flag.txt", "rb") as f:
flag = f.read()
msgs = [
b"I just cannot wait for rowing practice today!",
b"I hope we win that big rowing match next week!",
b"Rowing is such a fun sport!",
]
msgs.append(flag)
msgs *= 3
random.shuffle(msgs)
for msg in msgs:
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 3
m = bytes_to_long(msg)
c = pow(m, e, n)
with open("encrypted-messages.txt", "a") as f:
f.write(f"n: {n}\n")
f.write(f"e: {e}\n")
f.write(f"c: {c}\n\n")雖然他把一些訊息跟 Flag 打亂在一起了,不知道哪個才是我們要的。但可以看到他的公鑰指數e都固定設為 3,那就可以用小公鑰指數攻擊試試,把每一組都爆出來啦!接著我們看看密文encrypted-message.txt。
n: 12426348204210593270343924563278821305386892683425418957350363905840484905896816630189546938112358425679727243103082954824537007026886458498690134225705484501535835385800730412220192564706251228021192115494699150390312107794005569764411063907390563937247515046052549753641884721864426154021041082461015103337120756347692245843318676049947569653604616584167536958803278688355036036887022591104659059883622072052793378468850702811804337808760402077376453702190206077039468600466511349923882037572540505571672225260106649075841827340894515208811788428239691505001675042096850318994923571686175381862745049100863883977473
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393
n: 19928073532667002674271126242460424264678302463110874370548818138542019092428748404842979311103440183470341730391245820461360581989271804887458051852613435204857098017249255006951581790650329570721461311276897625064269097611296994752278236116594018565111511706468113995740555227723579333780825133947488456834006391113674719045468317242000478209048237262125983164844808938206933531765230386987211125968246026721916610034981306385276396371953013685639581894384852327010462345466019070637326891690322855254242653309376909918630162231006323084408189767751387637751885504520154800908122596020421247199812233589471220112129
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989
n: 13985338100073848499962346750699011512326742990711979583786294844886470425669389469764474043289963969088280475141324734604981276497038537100708836322845411656572006418427866013918729379798636491260028396348617844015862841979175195453570117422353716544166507768864242921758225721278003979256590348823935697123804897560450268775282548700587951487598672539626282196784513553910086002350034101793371250490240347953205377022300063974640289625028728548078378424148385027286992809999596692826238954331923568004396053037776447946561133762767800447991022277806874834150264326754308297071271019402461938938062378926442519736239
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989
n: 19594695114938628314229388830603768544844132388459850777761001630275366893884362012318651705573995962720323983057152055387059580452986042765567426880931775302981922724052340073927578619711314305880220746467095847890382386552455126586101506301413099830377279091457182155755872971840333906012240683526684419808580343325425793078160255607072901213979561554799496270708954359438916048029174155327818898336335540262711330304350220907460431976899556849537752397478305745520053275803008830388002531739866400985634978857874446527750647566158509254171939570515941307939440401043123899494711660946335200589223377770449028735883
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393
n: 12091176521446155371204073404889525876314588332922377487429571547758084816238235861014745356614376156383931349803571788181930149440902327788407963355833344633600023056350033929156610144317430277928585033022575359124565125831690297194603671159111264262415101279175084559556136660680378784536991429981314493539364539693532779328875047664128106745970757842693549568630897393185902686036462324740537748985174226434204877493901859632719320905214814513984041502139355907636120026375145132423688329342458126031078786420472123904754125728860419063694343614392723677636114665080333174626159191829467627600232520864728015961207
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664841337454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401
n: 19121666910896626046955740146145445167107966318588247850703213187413786998275793199086039214034176975548304646377239346659251146907978120368785564098586810434787236158559918254406674657325596697756783544837638305550511428490013226728316473496958326626971971356583273462837171624519736741863228128961806679762818157523548909347743452236866043900099524145710863666750741485246383193807923839936945961137020344124667295617255208668901346925121844295216273758788088883216826744526129511322932544118330627352733356335573936803659208844366689011709371897472708945066317041109550737511825722041213430818433084278617562166603
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273
n: 13418736740762596973104019538568029846047274590543735090579226390035444037972048475994990493901009703925021840496230977791241064367082248745077884860140229573097744846674464511874248586781278724368902508880232550363196125332007334060198960815141256160428342285352881398476991478501510315021684774636980366078533981139486237599681094475934234215605394201283718335229148367719703118256598858595776777681347337593280391052515991784851827621657319164805164988688658013761897959597961647960373018373955633439309271548748272976729429847477342667875183958981069315601906664672096776841682438185369260273501519542893405128843
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273
n: 11464859840071386874187998795181332312728074122716799062981080421188915868236220735190397594058648588181928124991332518259177909372407829352545954794824083851124711687829216475448282589408362385114764290346196664002188337713751542277587753067638161636766297892811393667196988094100002752743054021009539962054210885806506140497869746682404059274443570436700825435628817817426475943873865847012459799284263343211713809567841907491474908123827229392305117614651611218712810815944801398564599148842933378612548977451706147596637225675719651726550873391280782279097513569748332831819616926344025355682272270297510077861213
e: 3
c: 38999477927573480744724357594313956376612559501982863881503907194813646795174312444340693051072410232762895994061399222849450325021561935979706475527169503326744567478138877010606365500800690273
n: 21079224330416020275858215994125438409920350750828528428653429418050688406373438072692061033602698683604056177670991486330201941071320198633550189417515090152728909334196025991131427459901311579710493651699048138078456234816053539436726503461851093677741327645208285078711019158565296646858341000160387962592778531522953839934806024839570625179579537606629110275080930433458691144426869886809362780063401674963129711723354189327628731665487157177939180982782708601880309816267314061257447780050575935843160596133370063252618488779123249496279022306973156821343257109347328064771311662968182821013519854248157720756807
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664841337454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401
n: 22748076750931308662769068253035543469890821090685595609386711982925559973042348231161108618506912807763679729371432513862439311860465982816329852242689917043600909866228033526990181831690460395726449921264612636634984917361596257010708960150801970337017805161196692131098507198455206977607347463663083559561805065823088182032466514286002822511854823747204286303638719961067031142962653536148315879123067183501832837303731109779836127520626791254669462630052241934836308543513534520718206756591694480011760892620054163997231711364648699030108110266218981661196887739673466188945869132403569916138510676165684240183111
e: 3
c: 5065488652323342174251548936130018278628515304559137485528400780060697119682927936946069625772269234638180036633146283242714689277793018059046463458498115311853401434289264038408827377579534270489217094049453933816452196508276029690068611901872786195723358744119490651499187556193711866091991489262948739533990000464588752544599393
n: 15211900116336803732344592760922834443004765970450412208051966274826597749339532765578227573197330047059803101270880541680131550958687802954888961705393956657868884907645785512376642155308131397402701603803647441382916842882492267325851662873923175266777876985133649576647380094088801184772276271073029416994360658165050186847216039014659638983362906789271549086709185037174653379771757424215077386429302561993072709052028024252377809234900540361220738390360903961813364846209443618751828783578017709045913739617558501570814103979018207946181754875575107735276643521299439085628980402142940293152962612204167653199743
e: 3
c: 301927034179130315172951479434750678833634853032331571873622664841337454556713005601858152523700291841415874274186191308636935232309742600657257783870282807784519336918511713958804608229440141151963841588389502276162366733982719267670094167338480873020791643860930493832853048467543729024717103511475500012196697609001154401
n: 21920948973299458738045404295160882862610665825700737053514340871547874723791019039542757481917797517039141169591479170760066013081713286922088845787806782581624491712703646267369882590955000373469325726427872935253365913397944180186654880845126957303205539301069768887632145154046359203259250404468218889221182463744409114758635646234714383982460599605335789047488578641238793390948534816976338377433533003184622991479234157434691635609833437336353417201442828968447500119160169653140572098207587349003837774078136718264889636544528530809416097955593693611757015411563969513158773239516267786736491123281163075118193
e: 3
c: 86893891006724995283854813014390877172735163869036169496565461737741926829273252426484138905500712279566881578262823696620415864916590651557711035982810690227377784525466265776922625254135896966472905776613722370871107640819140591627040592402867504449339363559108090452141753194477174987394954897424151839006206598186417617292433784471465084923195909989
好!那既然看加密腳本已經發現了他的弱點,那就直接來寫 Exploit 吧。
import gmpy2
from Crypto.Util.number import long_to_bytes
def decrypt(cipher: dict) -> str:
e = cipher["e"]
n = cipher["n"]
c = cipher["c"]
k = 0
while True:
m, is_root = gmpy2.iroot(k * n + c, e)
if is_root:
break
else:
k += 1
return long_to_bytes(m).decode()
with open(r"encrypted-messages.txt", "r") as f:
file = f.read()
file = file.split("\n\n")
file.pop()
ciphers = []
for c in file:
cipher = {}
c = c.split("\n")
for item in c:
key, value = item.split(": ")
cipher[key] = int(value)
ciphers.append(cipher)
plaintext = ""
for cipher in ciphers:
plaintext += decrypt(cipher) + "\n"
print(plaintext)Voila! Flag 就出來啦~
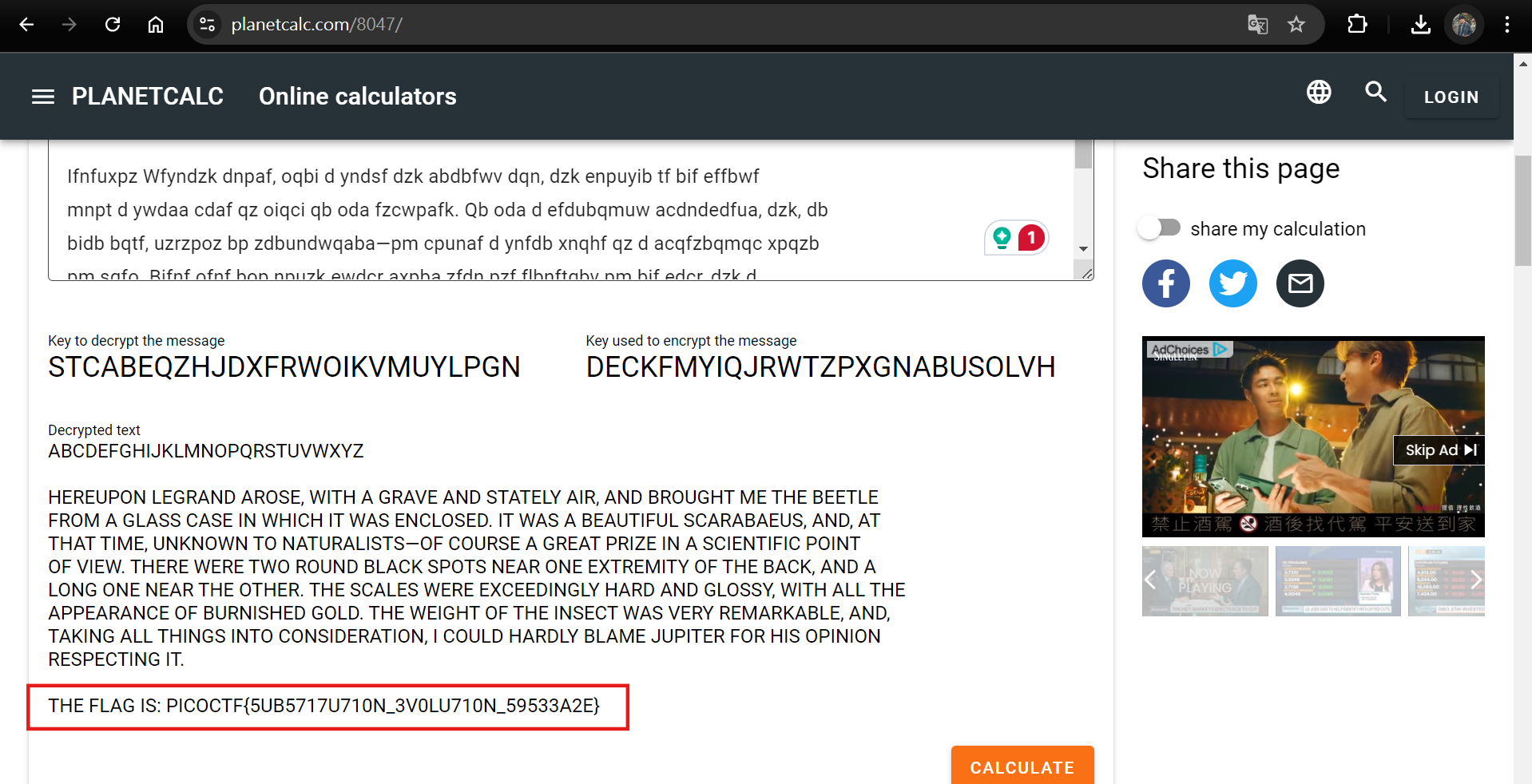
picoCTF{1_gu3ss_p30pl3_p4d_m3ss4g3s_f0r_4_r34s0n}substitution0
這題給了一個加密後的密文,如下。
DECKFMYIQJRWTZPXGNABUSOLVH
Ifnfuxpz Wfyndzk dnpaf, oqbi d yndsf dzk abdbfwv dqn, dzk enpuyib tf bif effbwf
mnpt d ywdaa cdaf qz oiqci qb oda fzcwpafk. Qb oda d efdubqmuw acdndedfua, dzk, db
bidb bqtf, uzrzpoz bp zdbundwqaba—pm cpunaf d ynfdb xnqhf qz d acqfzbqmqc xpqzb
pm sqfo. Bifnf ofnf bop npuzk ewdcr axpba zfdn pzf flbnftqbv pm bif edcr, dzk d
wpzy pzf zfdn bif pbifn. Bif acdwfa ofnf flcffkqzywv idnk dzk ywpaav, oqbi dww bif
dxxfdndzcf pm eunzqaifk ypwk. Bif ofqyib pm bif qzafcb oda sfnv nftdnrdewf, dzk,
bdrqzy dww biqzya qzbp cpzaqkfndbqpz, Q cpuwk idnkwv ewdtf Juxqbfn mpn iqa pxqzqpz
nfaxfcbqzy qb.
Bif mwdy qa: xqcpCBM{5UE5717U710Z_3S0WU710Z_59533D2F}最後一行看起來很像 Flag,但因為他給的是很大段的文字,所以可以直接去用暴力破解。我推薦使用這個網站,直接把整段輸入進去,他就會幫你找出最可能的解。
picoCTF{5UB5717U710N_3V0LU710N_59533A2E}substitution1
這題照理說應該跟上一題一樣,但是我覺得他題目可能有改過然後答案忘了改,因為我看了好多人的 writeup 都是這樣解,可是每個人的 Flag 都不一樣 XD,所以就先跳過了。
substitution2
這題也一樣用那個線上工具。
picoCTF{N6R4M_4N41Y515_15_73D10U5_42EA1770}ReadMyCert
這題給了一個 CSR (Certificate Signing Request) 文件,要我們去檢查這份文件。因為 CSR 文件的編碼方式是一種特定格式,不是單純的 Base64 編碼,我們可以用以下命令查看他。
openssl req -in <yourcsr.csr> -noout -text但為了方便,我們可以直接使用線上的 CSR Decoder幫我們解碼。
picoCTF{read_mycert_693f7c03}transposition-trial
先看題目敘述。
Our data got corrupted on the way here. Luckily, nothing got replaced, but every block of 3 got scrambled around! The first word seems to be three letters long, maybe you can use that to recover the rest of the message.
這代表每三個字為一個區塊,並且每個區塊都被相同的方式打亂了。密文長下面這樣。
heTfl g as iicpCTo{7F4NRP051N5_16_35P3X51N3_V091B0AE}2我們可以發現前三個字是The,所以能推測出他打亂的方式是每個 Block 中的最後一個變為第一個,其餘不變。那就來構造 Exploit 吧。
cipher = "heTfl g as iicpCTo{7F4NRP051N5_16_35P3X51N3_V091B0AE}2"
flag = ""
for i in range(0, len(cipher), 3):
block = cipher[i : i + 3]
flag += block[-1] + block[0:-1]
print(flag)這樣就出來啦!
picoCTF{7R4N5P051N6_15_3XP3N51V3_109AB02E}spelling-quiz
這題給了三個文件,encrypt.py、flag.txt和study-guide.txt。先來看看加密腳本。
import random
import os
files = [
os.path.join(path, file)
for path, dirs, files in os.walk(".")
for file in files
if file.split(".")[-1] == "txt"
]
alphabet = list("abcdefghijklmnopqrstuvwxyz")
random.shuffle(shuffled := alphabet[:])
dictionary = dict(zip(alphabet, shuffled))
for filename in files:
text = open(filename, "r").read()
encrypted = "".join([dictionary[c] if c in dictionary else c for c in text])
open(filename, "w").write(encrypted)可以看出他就是一個 Substitution Cipher。然後因為我們確定study-guide.txt裡面都是正常的單字(題目說的),所以我們可以直接把flag.txt接在study-guide.txt後面,接著拿去給一些線上工具解密就可以了(Frequency Attack)。這邊我用的是這個工具。
最後記得用picoCTF{}包起來。
picoCTF{perhaps_the_dog_jumped_over_was_just_tired}rail-fence
這題給了一個密文,如下。
Ta _7N6D8Dhlg:W3D_H3C31N__387ef sHR053F38N43DFD i33___N6他就是一個經典的柵欄密碼,可以直接拿去 線上工具 解密,記得要把下面這個選項開啟。然後就可以解出 Flag 啦。
picoCTF{WH3R3_D035_7H3_F3NC3_8361N_4ND_3ND_83F6D8D7}Dachshund Attacks
TODO: Wiener’s attack
from Crypto.Util.number import *
from pwn import *
import gmpy2
def continued_fraction(n, d):
"""Returns the continued fraction representation of a rational number n/d"""
cf = []
while d != 0:
cf.append(n // d)
n, d = d, n % d
return cf
def convergents(cf):
"""Returns the convergents from a continued fraction"""
n0, d0 = 0, 1
n1, d1 = 1, 0
convergents = []
for q in cf:
n2 = q * n1 + n0
d2 = q * d1 + d0
convergents.append((n2, d2))
n0, d0 = n1, d1
n1, d1 = n2, d2
return convergents
def wiener_attack(e, n):
"""Performs Wiener's attack using gmpy2 to recover d"""
cf = continued_fraction(e, n)
convs = convergents(cf)
for k, d in convs:
if k == 0:
continue
# Calculate phi using the convergent d
if (e * d - 1) % k == 0:
phi = (e * d - 1) // k
# Calculate the discriminant of the quadratic equation
b = n - phi + 1
discriminant = b**2 - 4 * n
if discriminant >= 0:
sqrt_disc = gmpy2.isqrt(discriminant)
if sqrt_disc * sqrt_disc == discriminant:
print(f"Private key found: d = {d}")
return d
return None
r = remote("mercury.picoctf.net", 37455)
r.recvuntil(b"e: ")
e = int(r.recvline().strip())
r.recvuntil(b"n: ")
n = int(r.recvline().strip())
r.recvuntil(b"c: ")
c = int(r.recvline().strip())
d = wiener_attack(e, n)
m = pow(c, d, n)
print(long_to_bytes(m))waves over lambda
這題連接上去後會吐密文,然後是個 Substitution cipher,直接拿去線上的詞頻分析破解他。
frequency_is_c_over_lambda_agflcgtyue然後這題並沒有用 picoCTF{} 包起來。

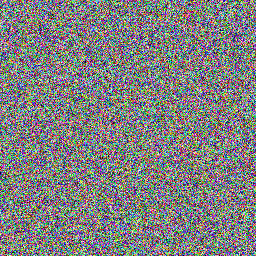
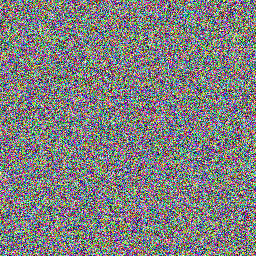


%20(1)_2fdc2382942f5aef8475bf32d3e8ab3d.jpg)






